Published: 18.12.2023
Idempotent Generative Networks
Introduction
Recently, I don't really recall how / by which medium, I stepped upon Idempotent Generative Network by Shocher et. al. The paper was very well written, presented a simple yet novel and elegant idea and kicked off with a funny quote:
GEORGE: You're gonna”overdry”it.
JERRY: You, you can't ”overdry.”
GEORGE: "Why not?"
JERRY: Same as you can't ”overwet.” You see, once something is wet, it's wet. Same thing with dead: like once you die you're dead, right? Let's say you drop dead and I shoot you: you're not gonna die again, you're already dead. You can't ”overdie,” you can't ”overdry.”
"Seinfield", Season 1, Episode 1, NBC 1989
Underneath the irony of this quote, there is an interesting idea: Some concepts are binary by nature. Something is either wet or dry. Someone is either dead or alive (Schrödinger's cat laughs in super-position). A sample is either in-distribution or out of distribution. So functions that bring this binary state to one of the two ends, like drying, are idempotent. If you dry something, it gets dry. If you dry it again, it will stay dry just as it was.
Driven by this last observation, the question (in the context of generative models) is: What if we learned a model that could "in-distribufy"? In other words, what if we enforced the fact that a prior distribution (random noise) has to be mapped to our data distribution, but things in-distribution cannot be made yet more in-distribution?
Then, we could draw something like this:
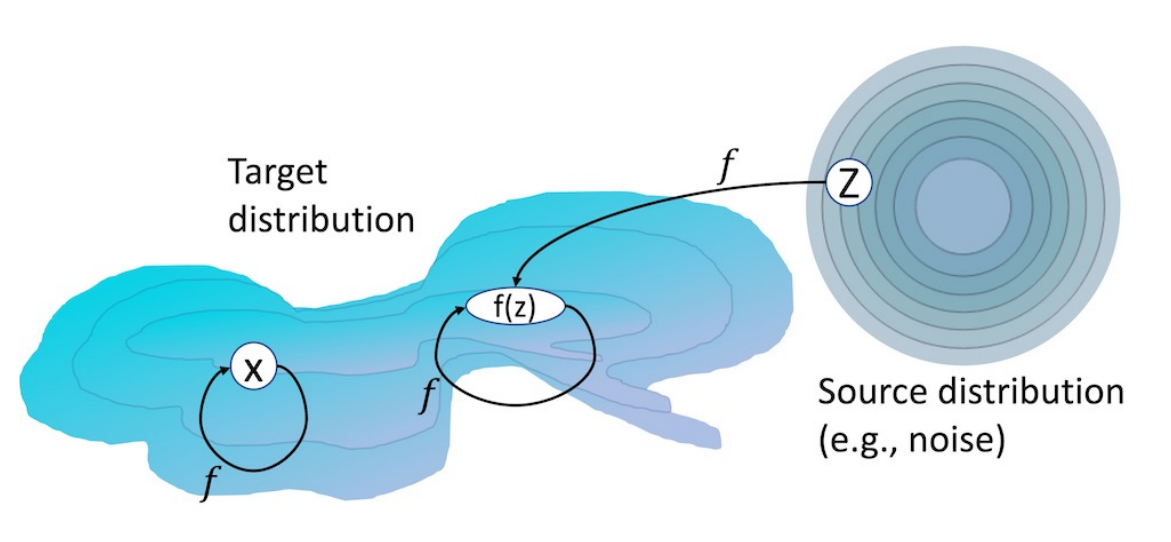
Figure 1 from Idempotent Generative Network by Shocher et. al.
where we have samples from a source distribution that have to be put in-distribution with a function , but has to leave in-distribution samples untouched. This gives rise to two objectives:
Reconstruction term
Idempotent term
where with the first, we encourage the function to give us back the same sample for in-disitribution samples, and with the second we encourage the function to be idempotent, that is, applying it twice should give the same effect as applying it just once (like when drying).
There is still something missing though: both objectives are perfectly satisfied if is the identity function. In fact, the identity function is the most basic idempotent function there is, and as of right now we are only optimizing for idempotence.
This is where the authors make the key observation that there are two pathways for the gradient: one, which is the desired one, encourages to put things into target distribution. In fact, if , since we already encourage we automatically have that . The other pathway instead, which we want to avoid, encourages to act as an identity regardless if the given input is in distribution or not. This is well represented with the second figure from the paper:
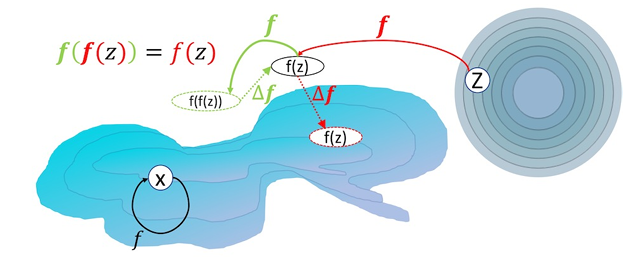
Figure 2 from Idempotent Generative Network by Shocher et. al.
In the figure, we see a data manifold in blue and the prior distribution as the sphere / circle. The red pathway pushes to be mapped onto the data manifold, where will also be enforced by . The green pathway is instead trying to map back to whatever we got in the first run, whether it was on the data manifold or not.
So the key idea now is to favour the good pathway, while discouraging the bad one. In this way, we get the desired behaviour out of the model by tightening the data manifold! This gives rise to a third term:
Tightening term
Which is the exact opposite of the idempotent term ...Wait, what?
Yes, we are in fact optimizing two exact opposing things. We want to make the function idempotent, but also to make it the exact opposite of idempotent. However, here's the catch: We want the function to be idempotent only within the data manifold, and to be quite the exact opposite of idempotent outside!
To do so, we encourage the model to output something that will remain the same whether it is mapped through a copy of the model again or not. At the same time, we encourage the model to map something that already went through the model once to something as different as possible.
This is perhaps better explained with an example. Let's assume that maps onto the data manifold. Then, despite the fact that we have one term trying to make , we also have two terms opposing this effect (the term on the inner part and the reconstruction term). Our function will act idempotent inside the data manifold.Let's now assume that maps out of distribution. We now have only one term fighting this effect, since the reconstruction term only works on the data manifold. Our function will thus try to map things closer to the data manifold.
Here is the total loss function:
where is any distance metric like L1, L2, etc... and we really only optimize , whereas for we use a copy of the model that we do not optimize. Ultimately, the total loss function is the sum of these terms weighted by some hyper-parameters:
Implementation
Given the simple yet elegant idea, and the fact that this could be tried quite quickly, I could not resist re-implementing this paper. My full re-implementation is available on GitHub.
The real highlight is the IdempotentNetwork lightning module, which can be used to train any model architecture using the above defined objectives:
1from copy import deepcopy
2
3from torch.optim import Adam
4from torch.nn import L1Loss
5import pytorch_lightning as pl
6
7
8class IdempotentNetwork(pl.LightningModule):
9 def __init__(
10 self,
11 prior,
12 model,
13 lr=1e-4,
14 criterion=L1Loss(),
15 lrec_w=20.0,
16 lidem_w=20.0,
17 ltight_w=2.5,
18 ):
19 super(IdempotentNetwork, self).__init__()
20 self.prior = prior
21 self.model = model
22 self.model_copy = deepcopy(model)
23 self.lr = lr
24 self.criterion = criterion
25 self.lrec_w = lrec_w
26 self.lidem_w = lidem_w
27 self.ltight_w = ltight_w
28
29 def forward(self, x):
30 return self.model(x)
31
32 def configure_optimizers(self):
33 optim = Adam(self.model.parameters(), lr=self.lr, betas=(0.5, 0.999))
34 return optim
35
36 def get_losses(self, x):
37 # Prior samples
38 z = self.prior.sample_n(x.shape[0]).to(x.device)
39
40 # Updating the copy
41 self.model_copy.load_state_dict(self.model.state_dict())
42
43 # Forward passes
44 fx = self(x)
45 fz = self(z)
46 fzd = fz.detach()
47
48 l_rec = self.lrec_w * self.criterion(fx, x)
49 l_idem = self.lidem_w * self.criterion(self.model_copy(fz), fz)
50 l_tight = -self.ltight_w * self.criterion(self(fzd), fzd)
51
52 return l_rec, l_idem, l_tight
53
54 def training_step(self, batch, batch_idx):
55 l_rec, l_idem, l_tight = self.get_losses(batch)
56 loss = l_rec + l_idem + l_tight
57
58 self.log_dict(
59 {
60 "train/loss_rec": l_rec,
61 "train/loss_idem": l_idem,
62 "train/loss_tight": l_tight,
63 "train/loss": l_rec + l_idem + l_tight,
64 },
65 sync_dist=True,
66 )
67
68 return loss
69
70 def validation_step(self, batch, batch_idx):
71 l_rec, l_idem, l_tight = self.get_losses(batch)
72 loss = l_rec + l_idem + l_tight
73
74 self.log_dict(
75 {
76 "val/loss_rec": l_rec,
77 "val/loss_idem": l_idem,
78 "val/loss_tight": l_tight,
79 "val/loss": loss,
80 },
81 sync_dist=True,
82 )
83
84 def test_step(self, batch, batch_idx):
85 l_rec, l_idem, l_tight = self.get_losses(batch)
86 loss = l_rec + l_idem + l_tight
87
88 self.log_dict(
89 {
90 "test/loss_rec": l_rec,
91 "test/loss_idem": l_idem,
92 "test/loss_tight": l_tight,
93 "test/loss": loss,
94 },
95 sync_dist=True,
96 )
97
98 def generate_n(self, n, device=None):
99 z = self.prior.sample_n(n)
100
101 if device is not None:
102 z = z.to(device)
103
104 return self(z)
105The model does just what we covered above: with l_rec we encourage the function to act as the identity for in-distribution samples, with l_idem we encourage the model to output something that will remain the same whether it is mapped through a copy of the model again or not and, finally, with l_tight we encourage the model to make input and output as different as possible (for when the model acts as a copy trying to disrupt its own output). This whole idea is quite unique and brilliant to be fair.
Now that we can train any model with the IGN objectives, we just need to write a classical training boilerplate code to try and generate MNIST digits. I went for my favourite stack: Pytorch Lightning with Weights and Biases:
1import os
2from argparse import ArgumentParser
3
4import torch
5from torch.utils.data import DataLoader
6from torchvision.datasets import MNIST
7from torchvision.utils import save_image
8from torchvision.transforms import Compose, ToTensor, Lambda
9import pytorch_lightning as pl
10from pytorch_lightning.loggers import WandbLogger
11from pytorch_lightning.callbacks import ModelCheckpoint
12
13from model import DCGANLikeModel
14from ign import IdempotentNetwork
15
16
17def main(args):
18 # Set seed
19 pl.seed_everything(args["seed"])
20
21 # Load datas
22 normalize = Lambda(lambda x: (x - 0.5) * 2)
23 noise = Lambda(lambda x: (x + torch.randn_like(x) * 0.15).clamp(-1, 1))
24 train_transform = Compose([ToTensor(), normalize, noise])
25 val_transform = Compose([ToTensor(), normalize])
26
27 train_set = MNIST(
28 root="mnist", train=True, download=True, transform=train_transform
29 )
30 val_set = MNIST(root="mnist", train=False, download=True, transform=val_transform)
31
32 def collate_fn(samples):
33 return torch.stack([sample[0] for sample in samples])
34
35 train_loader = DataLoader(
36 train_set,
37 batch_size=args["batch_size"],
38 shuffle=True,
39 collate_fn=collate_fn,
40 num_workers=args["num_workers"],
41 )
42 val_loader = DataLoader(
43 val_set,
44 batch_size=args["batch_size"],
45 shuffle=False,
46 collate_fn=collate_fn,
47 num_workers=args["num_workers"],
48 )
49
50 # Initialize model
51 prior = torch.distributions.Normal(torch.zeros(1, 28, 28), torch.ones(1, 28, 28))
52 net = DCGANLikeModel()
53 model = IdempotentNetwork(prior, net, args["lr"])
54
55 if not args["skip_train"]:
56 # Train model
57 logger = WandbLogger(name="IGN", project="Papers Re-implementations")
58 callbacks = [
59 ModelCheckpoint(
60 monitor="val/loss",
61 mode="min",
62 dirpath="checkpoints",
63 filename="best",
64 )
65 ]
66 trainer = pl.Trainer(
67 strategy="ddp",
68 accelerator="auto",
69 max_epochs=args["epochs"],
70 logger=logger,
71 callbacks=callbacks,
72 )
73 trainer.fit(model, train_loader, val_loader)
74
75 # Loading the best model
76 device = "cuda" if torch.cuda.is_available() else "cpu"
77 model = (
78 IdempotentNetwork.load_from_checkpoint(
79 "checkpoints/best.ckpt", prior=prior, model=net
80 )
81 .eval()
82 .to(device)
83 )
84
85 # Generating images with the trained model
86 os.makedirs("generated", exist_ok=True)
87
88 images = model.generate_n(100, device=device)
89 save_image(images, "generated.png", nrow=10, normalize=True)
90
91 print("Done!")
92
93
94if __name__ == "__main__":
95 parser = ArgumentParser()
96 parser.add_argument("--seed", type=int, default=0)
97 parser.add_argument("--lr", type=float, default=1e-4)
98 parser.add_argument("--batch_size", type=int, default=256)
99 parser.add_argument("--epochs", type=int, default=50)
100 parser.add_argument("--num_workers", type=int, default=8)
101 parser.add_argument("--skip_train", action="store_true")
102 args = vars(parser.parse_args())
103
104 main(args)At first, I found training of IGNs to be unstable. I suspected this might be the case, since we basically have an instance of adversarial training. With adversarial training, like in GANs, you might face the problem where the two actors keep on changing, entering a loop where neither converges because each one has to adapt to the moving counterpart.
However, I was skeptical of the model used in this work, DCGAN from Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks by Radford et. al., which being from 2015 is stone-age old and does not include modern architectural choices. For example, it completely lacks dropout and normalization layers, as well as residual connections, which are key to any model nowadays. While no big models are needed to generate MNIST digits, doing without these core components felt wrong. I suspected that this might further harm training stability, so I opted to add batch normalizations and dropout layers here and there.
1"""DCGAN code from https://github.com/kpandey008/dcgan"""
2import torch.nn as nn
3
4
5class Discriminator(nn.Module):
6 def __init__(self, in_channels=1, base_c=64):
7 super(Discriminator, self).__init__()
8 self.main = nn.Sequential(
9 # Input Size: 1 x 28 x 28
10 nn.Conv2d(in_channels, base_c, 4, 2, 1, bias=False),
11 nn.Dropout2d(0.1),
12 nn.LeakyReLU(negative_slope=0.2, inplace=True),
13 # Input Size: 32 x 14 x 14
14 nn.BatchNorm2d(base_c),
15 nn.Conv2d(base_c, base_c * 2, 4, 2, 1, bias=False),
16 nn.Dropout2d(0.1),
17 nn.LeakyReLU(negative_slope=0.2, inplace=True),
18 # Input Size: 64 x 7 x 7
19 nn.BatchNorm2d(base_c * 2),
20 nn.Conv2d(base_c * 2, base_c * 4, 3, 1, 0, bias=False),
21 nn.Dropout2d(0.1),
22 nn.LeakyReLU(negative_slope=0.2, inplace=True),
23 # Input Size: 128 x 7 x 7
24 nn.BatchNorm2d(base_c * 4),
25 nn.Conv2d(base_c * 4, base_c * 8, 3, 1, 0, bias=False),
26 nn.Dropout2d(0.1),
27 nn.LeakyReLU(negative_slope=0.2, inplace=True),
28 # Input Size: 256 x 7 x 7
29 nn.Conv2d(base_c * 8, base_c * 8, 3, 1, 0, bias=False),
30 )
31
32 def forward(self, input):
33 return self.main(input)
34
35
36class Generator(nn.Module):
37 def __init__(self, in_channels=512, out_channels=1):
38 super(Generator, self).__init__()
39 self.main = nn.Sequential(
40 # Input Size: 256 x 7 x 7
41 nn.BatchNorm2d(in_channels),
42 nn.ConvTranspose2d(in_channels, in_channels // 2, 3, 1, 0, bias=False),
43 nn.Dropout2d(0.1),
44 nn.ReLU(True),
45 # Input Size: 128 x 7 x 7
46 nn.BatchNorm2d(in_channels // 2),
47 nn.ConvTranspose2d(in_channels // 2, in_channels // 4, 3, 1, 0, bias=False),
48 nn.Dropout2d(0.1),
49 nn.ReLU(True),
50 # Input Size: 64 x 7 x 7
51 nn.BatchNorm2d(in_channels // 4),
52 nn.ConvTranspose2d(in_channels // 4, in_channels // 8, 3, 1, 0, bias=False),
53 nn.Dropout2d(0.1),
54 nn.ReLU(True),
55 # Input Size: 32 x 14 x 14
56 nn.BatchNorm2d(in_channels // 8),
57 nn.ConvTranspose2d(
58 in_channels // 8, in_channels // 16, 4, 2, 1, bias=False
59 ),
60 nn.Dropout2d(0.1),
61 nn.ReLU(True),
62 # Input Size : 16 x 28 x 28
63 nn.ConvTranspose2d(in_channels // 16, out_channels, 4, 2, 1, bias=False),
64 nn.Tanh(),
65 # Final Output : 1 x 28 x 28
66 )
67
68 def forward(self, input):
69 return self.main(input)
70
71
72class DCGANLikeModel(nn.Module):
73 def __init__(self, in_channels=1, base_c=64):
74 super(DCGANLikeModel, self).__init__()
75 self.discriminator = Discriminator(in_channels=in_channels, base_c=base_c)
76 self.generator = Generator(base_c * 8, out_channels=in_channels)
77
78 def forward(self, x):
79 return self.generator(self.discriminator(x))
80Surprisingly, this fixed the stability issues during training, although I would not be surprised if training IGNs would turn out to be difficult for some datasets.
Here I share the Weights and Biases run of the final model that I used to generate MNIST digits.
And of course, ✨ dulcis in fundo ✨, here are the generated images:

Generated images with Idempotent Generative Network
Thank you for reading! If you found this helpful / interesting, or have suggestions on how to improve, please do not hesitate to contact me at me@brianpulfer.ch